If done naively, such an n-body simulation has a runtime complexity of O(n^2) because we need to consider the interaction of every body with every other body. Barnes-Hut performs an approximation that reduces this to O(n . log n). At each step in the simulation we insert the bodies (grey) into a quad-tree (green), and compute the centroid for each branch (blue). Now, if some other body is sufficiently far away from a centroid, then we use the centroid to approximate the force due to the bodies in the corresponding branch, instead of inspecting each one individually.
Now you've seen the video, the following graph sums up my work on Data Parallel Haskell (DPH) for the past six months:
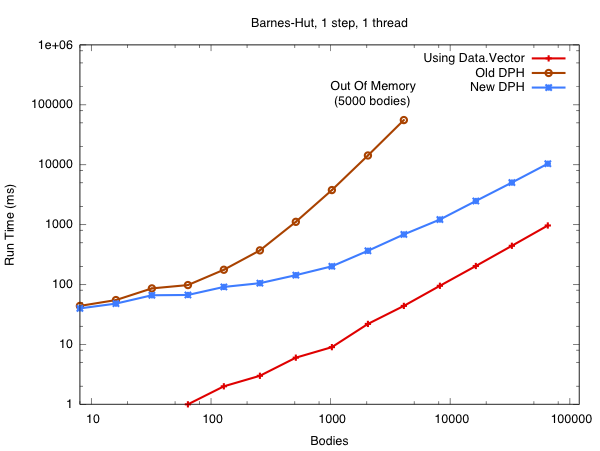
This is a plot of runtime vs the number of bodies in the Barnes-Hut simulation. The simulation in the video uses just 1000 bodies, but my understanding is that the physicists need millions or billions to do useful physics work. Back to the graph, the red line is the program from the video, which uses Data.Vector to store its arrays and runs sequentially. The brown line is using the DPH library that shipped with GHC 7.2. The blue line is using the DPH library that will ship with GHC 7.4. Note how the asymptotic complexity of the program with New DPH is the same as with Data.Vector.
In Old DPH we were using a naive approach to vectorisation that resulted in the quad-tree being replicated (copied) once for every body in the simulation (bad!). In New DPH we compute the force on each body in parallel while sharing the same quad-tree. There is a story about this, and you can read all about it when we finish the paper.
Of course, asymptotic complexity isn't everything. The DPH program is still running about 10x slower than the Data.Vector program for large input sizes, and I'm sure that production C programs would run at least 5x faster than that. There's much low hanging fruit here. DPH misses many standard optimisation opportunities, which results in numerical values being unboxed and reboxed in our inner loops. There are also algorithmic improvements to the library that are just waiting for me to implement them. If I can make the blue line cross the red line in the next six months, then I'm buying everyone a beer.
Manuel's slides describing the replicate problem are available in HTML5 slideshow and PDF.
ReplyDeleteFree No Deposit Casinos 2021
ReplyDeleteNew or existing players 유로스타사이트 only, welcome bonus of 100,000 or a 토토 사이트 추천 100% match. Deposit Methods: BONUS tenpro CODE, EBT-CASH, BONUS 7 포커 족보 CODE, 룰렛 사이트 LATAB.